Impfungen, Übersterblichkeit - und statistische Nebelbomber

Der ARD-Kabarettist Dieter Nuhr macht sich öffentlich darüber lustig, ZIB-2-Anchorman Armin Wolf twittert dazu. Der Epidemiologe Gerald Gartlehner schickt mir eine mahnende Mail: "Herr Kuhbandner, der ja prominent in Ihrer Doku war, hat es nun geschafft mit seinen Auswertungen als 'Unstatistik des Monats' gekürt zu werden." Was ist passiert? - Widmen wir uns der Analyse einer öffentlichen Reaktion auf einen alarmierenden Befund. 

Geht von den Covid-Impfungen ein relevantes Krankheits- und Sterberisiko aus? Diese Frage hat nach vielen Wochen intensiver Forschungstätigkeit der bayrische Wissenschaftler Christof Kuhbandner aufgeworfen. Bereits vor Weihnachten hatte er die Behörden über seine brisanten Analysen informiert, stieß jedoch sowohl beim Paul-Ehrlich-Institut als auch beim Robert Koch-Institut auf taube Ohren. 

Weil die Zeit drängte, stellte Kuhbandner seine statistischen Analysen inklusive der Rohdaten öffentlich zur Verfügung. Er lud andere Wissenschaftler ein, seine Rechengänge nachzuprüfen und in eine fachliche Diskussion einzusteigen. "Denn wenn sich bestätigen sollte, dass hier ein kausaler Effekt der Impfungen abgebildet wird, dann haben wir es mit einer extrem alarmierenden Situation zu tun: dann haben wir tausende von Menschen, die möglicherweise an den Impfungen versterben, ohne dass man sich dessen bewusst ist."

Das Echo auf sein Interview in der von mir gestalteten Servus TV Doku war enorm. Er erhielt hunderte von Mails - darunter auch einige Zuschriften von anderen Wissenschaftlern, die in ihren eigenen Arbeiten auf ähnliche Resultate gestoßen sind. Mittlerweile hat sich eine internationale Arbeitsgruppe etabliert, die mit unterschiedlichen Zugängen in verschiedenen Ländern den möglichen Zusammenhang prüft. Die Korrelation zwischen der Anzahl der täglichen Impfdosen und der wenig später parallel dazu ansteigenden Sterbeziffern ist jedenfalls bei weitem nicht nur auf Deutschland beschränkt. 

Natürlich bedeutet Korrelation nicht, dass damit automatisch eine Kausalität verbunden ist. Dies betont Kuhbandner in jeder Stellungnahme und es steht auch mehrfach in seiner Veröffentlichung. Aber Kausalität bedeutet Korrelation. Sollte ein Medikament bisher unbekannte Nebenwirkungen hervorrufen, dann bildet sich das in einer Korrelation ab: Mit der zunehmenden Verabreichung des Medikaments wird die Nebenwirkung zunehmend häufiger beobachtet. 

Es ergeben sich in diesem Fall also zwei nicht-stationäre Zeitreihen - also Zeitreihen mit einem zeitlichen Trend – die gemeinsam ansteigen. Aus der Tatsache, dass es bei unabhängigen nicht-stationären Zeitreihen per Zufall hohe Korrelationen geben kann, zu schließen, bei der beobachteten Korrelation zwischen der Medikamentverabreichung und der vom Medikament kausal erzeugten Nebenwirkung handle es sich um eine „spurious Correlation“ - also Zufall - wäre absurd und gefährlich. 

Und genau deswegen ist die Beobachtung, dass eine Krankheit im zeitlichen Zusammenhang mit der Verabreichung eines Medikamentes plötzlich ansteigt, ein Sicherheitssignal: Dann steht die Möglichkeit im Raum, dass es eine bisher unbekannte Nebenwirkung gibt. Da Korrelation nicht Kausalität bedeuten muss, ist das natürlich nur ein erstes Warnsignal, das dann mit weiteren Studien genauer untersucht werden muss. Korrelationen stellen also ein Frühwarn-System dar, das die Formulierung von Hypothesen ermöglicht, die anschließend mit weitergehenden Methoden geprüft und verifiziert - oder eben falsifiziert - werden können.

Dies wäre der seriöse Weg gewesen, mit den von Kuhbandner aufgeworfenen Fragen umzugehen. 

Seit einigen Tagen haben nun aber offenbar die Witzbolde das Regiment übernommen. Der Kabarettist Dieter Nuhr widmet sich in seinem Format "Nuhr im Ersten" Kuhbandners Analyse und bringt gleich eine ganze Abfolge an kuriosen Korrelationen, die ebenso ernst zu nehmen wären, wie Kuhbanders Verknüpfung von Impfquote und Sterberisiko: Beispielsweise den Margarine-Konsum in den USA und die Scheidungsrate im Bundesstaat Maine. Oder den Rindfleischkonsum pro Kopf und Todesfälle durch Blitzschlag. 

Auch Armin Wolf ist ganz entzückt über die Sinnlos-Korrelationen und steuert ein Beispiel bei, wonach die Zahl der Menschen, die in Swimming-Pools ertrinken offenbar irgendwie mit der Anzahl der Filmrollen von Nicholas Cage zusammen hängt. Hier sein Tweet: 

Dieser Vergleich bringt Wolf unmittelbar zu Kuhbandners Analyse. 

 

Wolf und Nuhr bezogen sich in ihren Beiträgen auf das "Leibnitz Institut für Wirtschaftsforschung" (RWI-Essen), welche Kuhbandners Analyse kurz davor zur "Unstatistik des Monats" erklärt hatte. Und zwar mit dem Hinweis, dass es sich bei dem von ihm gefundenen Zusammenhang zweifellos um eine "spurious correlation" handle - also eine "Nonsense-Korrelation". 

So etwas, erklären Thomas Bauer und Katharina Schüller, die Autoren der "Unstatistik", kann man massenhaft beobachten, wenn man bloß ein wenig sucht: "So erhält man beispielsweise in den USA eine nahezu perfekte Korrelation zwischen der Anzahl von Personen die jährlich gestorben sind, weil sie sich in ihrem Bettlaken verheddert haben, und dem durchschnittlichen jährlichen Pro-Kopf-Käsekonsum."

Dass solche Nonsense-Korrelationen existieren, ist natürlich absolut richtig. Aber daraus zu schließen, beim beobachteten zeitlichen Zusammenhang der Übersterblichkeit mit den COVID-Impfungen würde es sich ebenfalls um eine Nonsense-Korrelation handeln, ist ein gefährlicher Fehlschluss. Natürlich muss Korrelation nicht Kausalität bedeuten. Aber gleichzeitig bilden sich bisher unbekannte Nebenwirkungen eines Medikaments wie oben beschrieben notwendigerweise in einer Korrelation ab. Würde man solche beobachteten Korrelationen einfach immer mit dem Verweis auf existierende Scheinkorrelationen beiseite wischen, würde man unbekannte Nebenwirkungen niemals entdecken.

Auch die weitere Argumentation in der 'Unstatistik des Monats' ist zu hinterfragen. Statt auf solche Nonsense Korrelationen reinzufallen, empfehlen Bauer und Schüller, den Blick nach Österreich zu werfen, denn hier existiere - anders als in Deutschland - ein Impfregister, "so dass man den Einfluss einer Impfung auf die Wahrscheinlichkeit zu versterben auf Personenebene analysieren kann." - Und die Österreicher, so die "Unstatistiker" triumphierend, haben nunmal nachgewiesen, dass „Ungeimpfte ein signifikant höheres Sterberisiko haben als jene, die zumindest eine Impfdosis erhalten haben“.

In dieser Aussage sind gleich mehrere Fehler. Österreich hat nämlich kein Impfregister, das die Verknüpfung des Impfstatus mit personenbezogenen Gesundheitsdaten ermöglicht. Stattdessen laboriert Österreich - ähnlich wie Deutschland - an einem Datenchaos, speziell im Bezug auf die Covid-relevanten Informationen. Hier wären – als kleiner Recherche Tipp an die Leibnitzer Wirtschaftsforscher – ein ganzer Schatz an "Unstatistiken" zu bergen. Dafür müssten sie sich allerdings mit den Behörden - und der Politik - anlegen und das würde etwas Zivilcourage erfordern. Da ist es doch wesentlich einfacher, über einen einzelnen Wissenschaftler herzufallen, der das allseits gepflegte Narrativ der heilbringenden Impfung beschmutzt. 

Die "Unstatistiker" haben sich ihre Analyse auch insofern recht leicht gemacht, als sie den Großteil ihrer Argumentation aus einem Tweet des Statistikers Dominik Liebl übernommen haben - übrigens ohne diese "Inspiration" zu erwähnen. 

Dominik Liebl ist Professor am Institut für Finanz und Statistik der Universität Bonn. Trotz dieser - nicht eben medizin-nahen - Position eröffnete er in einem Tweet das Feuer auf Kuhbandner. 

Sehen wir uns also an, wie Dominik Liebl, argumentiert. Zunächst fällt sofort auf, wie hier von Anfang an ein sehr abwertendes Framing gewählt wird: 

Danach wird ausschnitthaft ein Einzelbefund gezeigt, in dem der zeitliche Zusammenhang – anders als bei vielen der weiteren Zusammenhangsbefunde – visuell besonders schwer zu sehen ist und zudem – anders als bei den weitergehenden Analysen von Kuhbandner – durch mögliche saisonale Effekte erklärt werden kann:

Hier ist als Vergleich die Befundlage zu den Erstimpfungen (gelber Rahmen, ab dann kommen die Zweitimpfungseffekte dazu). Die obere Graphik zeigt den beobachteten zeitlichen Zusammenhang der Erstimpfungen mit der Anzahl der Todesfälle (alle Ursachen), die mittlere Graphik den zeitlichen Zusammenhang mit der Übersterblichkeit (Zuwachs an Todesfällen im Vergleich zum Durchschnitt der fünf Vorjahren) und die untere Graphik den zeitlichen Zusammenhang mit der nicht durch COVID bedingten Übersterblichkeit (Quelle).

Wie die obere Graphik zeigt, steigt mit der Anzahl der Erstimpfungen die Anzahl der Todesfälle (alle Todesursachen) nahezu parallel an, jeder „Zacken“ in der Impfkurve findet sich in der Kurve der Todesfälle wieder. Dasselbe Muster findet man, wenn man die Übersterblichkeit – im Sinne der Zunahme der Todesfälle im Jahr 2021 im Vergleich zum Durchschnitt der fünf Vorjahre – betrachtet, das zeigt die mittlere Graphik. Das heißt: Saisonale Effekte können den beobachteten Zusammenhang nicht erklären. Die untere Graphik zeigt den Zusammenhang zwischen den Impfungen und den nicht durch COVID bedingten Todesfällen. Auch hier zeigt sich ein starker zeitlicher Zusammenhang, das heißt: Der beobachtete Zusammenhang kann auch nicht durch COVID-bedingte Effekte wie die Anzahl der SARS-CoV-2-Infektionen oder die Anzahl der COVID-Todesfälle erklärt werden (es sei denn, man würde ohne jede Evidenz dafür annehmen, dass es sich bei den Non-COVID-Todesfällen um nicht erkannte COVID-Todesfälle handeln würde).

Danach kommt in Liebls Tweet das von der „Unstatistik“ übernommene fragwürdige Argument, aus der Tatsache, dass bei unabhängige nicht-stationären Zeitreihen manchmal hohe positive Korrelationen per Zufall auftreten, könne man schließen, dass es sich beim beobachteten zeitlichen Zusammenhang zwischen den Impfungen und den Todesfällen um eine „spurious Correlation“ handle.

Der Tweet schließt schließlich mit einer weiteren hochmütigen Diffamierung:

Trotz dieser diffamierend aufbereiteten Kritik nimmt Christof Kuhbandner mit Dominik Liebl Kontakt auf um über die Sachlage zu diskutieren. Dieser schreibt zurück. Nach einigen Mails twittert Liebl dies hier:

Liebls Vorwurf lautet demnach, Kuhbandner sei nicht an der "tatsächlichen Aussagekraft der eigenen Analyse interessiert".

Dann machen wir uns doch selbst ein Bild, wer hier woran interessiert - oder nicht interessiert - ist.

Im folgenden bringe ich - mit Einverständnis von Christof Kuhbandner und Dominik Liebl - deren Email-Austausch. 

Dabei wiederholt Liebl ein ums andere Mal seinen Vorwurf der Scheinkorrelation. Kuhbandner bringt eine Reihe von zusätzlichen Beispielen, verweist auf Irrtümer geht auf fachliche Details ein.

Aber seht selbst.
Den Anfang macht diese Mail Kuhbandners als Reaktion auf Liebls Tweet über das "gruselig schlechte Paper":

>>> Christof Kuhbandner 26.01.2022, 01:30 >>>

Sehr geehrter Herr Liebl,

ich habe gesehen, dass Sie in einem Twitter-Beitrag auf den Befund des zeitlichen Zusammenhangs zwischen der Übersterblichkeit und den COVID-Impfungen eingegangen sind:

Ich schätze Ihre Arbeiten wirklich sehr und habe Ihre Twitter-Beiträge immer mit großem Interesse gelesen. Aber in diesem Fall muss ich mich bei Ihnen melden, um Ihre Argumente besser nachvollziehen zu können. Ich würde mich wirklich sehr freuen, wenn Sie mir hier antworten würden.

Ich möchte hier gerne vorneweg schicken, dass es mir hier ausschließlich darum geht, das beobachtete Befundmuster zum zeitlichen Zusammenhang zwischen der Übersterblichkeit und den Impfungen besser zu verstehen. Sie scheinen - zumindest so wie Sie Ihren Twitter-Beitrag an manchen Stellen framen - davon auszugehen, dass ich hier irgendeine vorgefertigte Sichtweise hätte, die ich mit irgendwelchen statistischen Mitteln abzusichern versuchen würde. Ich kann Ihnen wirklich versichern, dass ich hier ausschließlich daran interessiert bin, die Dinge so fundiert wie möglich aufzuarbeiten. Sollte es wirklich irgendeine nachvollziehbare Alternativerklärung geben, welche den existierenden zeitlichen Zusammenhang zwischen der Übersterblichkeit und den Impfungen alternativ erklären kann, wäre ich absolut erleichtert.

Als Ausgangsbasis möchte ich hier als Beispiel den beobachteten zeitlichen Zusammenhang zwischen der Übersterblichkeit (Zuwachs an Todesfällen im Jahr 2021 im Vergleich zum Durchschnitt der fünf Vorjahre) und den Erstimpfungen noch einmal darstellen. Dieser sieht so aus:

Wenn ich es richtig sehe, argumentieren Sie hier folgendermaßen:

1. Bei der Zeitreihe der Erstimpfungen und der Zeitreihe der Übersterblichkeit handelt es sich um zwei nicht stationäre Zeitreihen.
2. Bei nicht stationären Zeitreihen gibt es sehr oft große Korrelationskoeffizienten von nahe + oder - 1.
3. Daraus schließen Sie, dass es sich bei der sehr starken zeitlichen Kovariation der Zeitreihe der Übersterblichkeit und der Zeitreihe der Erstimpfungen um eine "spurious correlation" handeln würde, und in Wirklichkeit die Übersterblichkeit mit den Impfungen nicht zusammenhängen würde.

Aber wenn ich es richtig sehe, treffen zwar (1) und (2) zu, der daraus gezogene Schluss (3) ist aber wissenschaftlich gesehen nicht valide.

Das kann man sich beispielsweise anhand eines einfachen Gedankenexperiments klarmachen:

Nehmen wir rein theoretisch an, es wäre so, dass die Impfungen kausal die Übersterblichkeit erhöhen und beispielsweise pro 1.000 Impfungen ein zusätzlicher Todesfall auftritt, der sonst nicht beobachtet worden wäre. Dann würde man zwei nicht stationäre Zeitreihen beobachten, die exakt kovariieren. Hier zu schließen, dieser Zusammenhang wäre „spurious“ weil es sich um zwei nicht stationäre Zeitreihen handelt, und der kausale Zusammenhang zwischen der Übersterblichkeit und den Impfungen wäre damit nicht existent, wäre ein irreführender Fehlschluss.

Dass es sich hier nicht um zufällig und unsystematisch auftretende hohe Korrelationen handelt, legt beispielsweise eine Analyse der zeitlichen Kovariation zwischen der Übersterblichkeit und den Erstimpfungen getrennt für die 16 Bundesländer nahe. Dort wurde jeweils etwas unterschiedlich geimpft, es finden sich also immer leicht unterschiedliche Impf-Zeitreihen. Interessanterweise variiert die jeweils beobachtete Übersterblichkeit pro Bundesland jeweils sehr spezifisch mit dem jeweils in einem bestimmten Bundesland vorgefundenen Impfverlauf, wie in der folgenden Abbildung für die Erstimpfungen gezeigt (die Bundesländer sind absteigend nach der Größe geordnet, weil die Übersterblichkeit umso zuverlässiger geschätzt wird, je größer das Bundesland ist):

Ich würde mich wirklich sehr freuen, Ihre Einschätzung dazu zu hören. Mir geht es hier wirklich ausschließlich darum, das besorgniserregende Muster, das hier zu beobachten ist, so gut wie möglich zu verstehen, und im besten Falle auszuschließen, dass der beobachtete zeitliche Zusammenhang zwischen der Übersterblichkeit und den Impfungen einen kausalen Effekt der Impfungen widerspiegelt.

Und wenn Sie hier konkrete statistische Analysevorschläge haben, wie man Ihrer Meinung nach solche Daten bestmöglich analysiert, können Sie mir diese auch sehr gerne mitteilen, da ich gerade mit einem internationalen Team an Wissenschaftlern und Statistikern dabei bin, diese Daten tiefergehend zu analysieren.

Herzliche Grüße

Christof Kuhbandner

>>> Dominik Liebl <dliebl@uni-bonn.de> 26.01.2022, 09:26 >>>

Sehr geehrter Herr Kuhbandner, 

wenn Sie meine Beiträge verfolgen, werden Sie ja wissen, dass ich durchaus kritisch bin, was die Corona-Politik und deren wissenschaftliche Rechtfertigungen angeht. 

Wenn Sie zeigen wollen, dass es einen Zusammenhang zwischen Impfungen und Todeszahlen gibt, dann müssen Sie das eben methodisch richtig machen. Aus Ihren Analysen folgt kein "Starker Zusammenhang". Die hohen Korrelationen folgen aus der Nicht-stationarität der Zeitreihen. Das methodische Problem habe ich ja beschrieben. Zur Einordnung: Da dies eine übliche methodische Falle bei nicht-stationären Zeitreihen ist, thematisiert man dieses Problem bei jeder vernünftigen Zeitreihenvorlesung - auch schon auf Bachelor-Niveau. 

Die häufigste Lösung des methodischen Problems:
Transformieren Sie die nicht-stationären Zeitreihen in stationären Zeitreihen mittels Differenzenbildung. Die ursprünglichen Zeitreihen werden so verwandelt in Zeitreihen von Änderungen. Korrelieren Sie dann die stationären Zeitreihen miteinander. Erst dann berechnen sie eine Korrelation und keine Scheinkorrelation. Sollte es einen Zusammenhang geben, so sieht man den auch in den Änderungen. Gegeben Sie haben dann eine „Starken Zusammenhang“, müssen Sie noch argumentieren, warum Korrelation hier evtl. Kausalität ist.  

Um eine evtl. Frage vorwegzunehmen: Nein, ich kann diese Analyse nicht für Sie machen. Sie haben sehr gute Statistiker an der Uni Regensburg. Sprechen Sie doch mit einem von diesen.  

Mit freundlichen Grüßen

Dominik 

>>> Christof Kuhbandner 26.01.2022, 17:43 >>>

Sehr geehrter Herr Liebl,

es freut mich sehr, hier von Ihnen eine Antwort zu erhalten. Aber leider muss ich mich nochmals melden, da Sie auf den in Ihrem Twitter-Beitrag in meinen Augen existierenden Fehlschluss leider bisher nicht eingegangen sind. Vielmehr wiederholen Sie denselben Fehlschluss im Grunde in Ihrer Email noch einmal.

Hier ist ein Screenshot Ihres Beitrags:

Auch in der Email an mich formulieren Sie wieder: „Die hohen Korrelationen folgen aus der Nicht-stationarität der Zeitreihen“.

Wie schon in meiner ersten Email an Sie ausgeführt: Das ist nichts anderes als eine reine, nicht wissenschaftlich valide Spekulation von Ihnen, die Sie einfach nur daraus ableiten, dass zwei nicht stationäre Zeitreihen oft hohe Korrelationen von 1 oder -1 aufweisen. Die hohe Korrelation kann aber genauso aus einem kausalen Effekt der einen Zeitreihe auf die andere Zeitreihe folgen, das kann man prinzipiell nicht ausschließen. Wie bereits anhand des Gedankenexperiments illustriert (siehe meine vorherige Email), muss eine nicht stationäre Zeitreihe bei einem kausalen Effekt notwendigerweise eine zweite nicht stationäre Zeitreihe erzeugen. Ihre Aussage, die hohe Korrelation würde aus der Nicht-Stationarität der Zahlen folgen, wäre in diesem Fall dann ganz einfach inhaltlich falsch.

Man kann das sogar noch etwas weiter ausführen. Sie zeigen ja in Ihrem Twitterbeitrag die folgende Graphik zur Verteilung der Korrelationskoeffizienten bei nicht stationären unabhängigen Zeitreihen:

Rein theoretisch variiert - wenn man nicht stationäre unabhängige Zeitreihen sozusagen zufällig gegeneinander verschiebt - der Korrelationskoeffizient zwischen -1 und +1 in Form einer U-förmigen Verteilung. Aber - und das zeigt ja gerade die Graphik sehr schön: (1) es gibt durchaus auch kleinere Korrelationen und (2) es gibt insbesondere auch viele negative Korrelationen. Hoch positive Korrelationen gibt es nur dann, wenn die beiden Zeitreihen zufällig einigermaßen aufeinanderliegen, was aber nur bei einem kleineren Teil der aus der Zufallsverschiebung der Zeitreihen resultierenden Muster der Fall ist:

Es muss also nicht notwendigerweise der Fall sein, dass sich aus nicht stationären Zeitreihen hohe positive Korrelationen ergeben. Im Grunde ist die Wahrscheinlichkeit einer wirklich hoch positiven Korrelation bei einem Zufallsmuster sogar eher vergleichsweise klein.

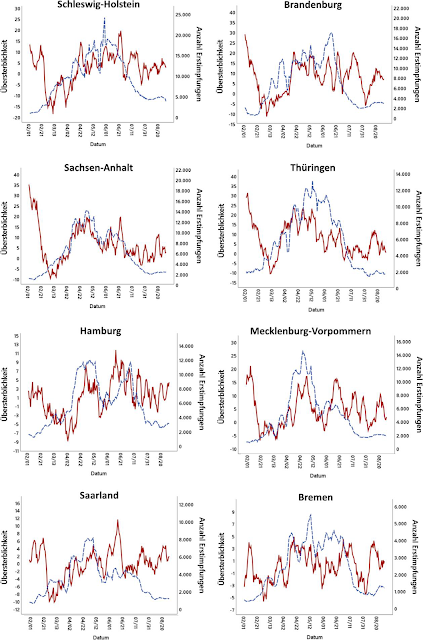
Wie ich Ihnen beschrieben hatte, sind hier insbesondere die zusätzlichen Analysen auf Bundeslandebene interessant, weil selbst bei einem Split der Gesamtdaten in die 16 Bundesländer die beiden Zeitreihen der Übersterblichkeit und der Impfungen jeweils noch immer aufeinanderliegen, obwohl der Impfverlauf von Bundesland zu Bundesland variiert. Das spricht ganz klar gegen einen reinen Zufallseffekt bei nicht stationären Zeitreihen.

Man kann sich auch auf die Suche nach weiterer empirischer Evidenz machen, beispielsweise, in dem man weitere Zeitreihen zu möglichen Impfschäden betrachtet. Sollten diese ebenfalls hoch positiv mit dem Verlauf der Impfungen korrelieren, ist das als weitere Evidenz zu werten, dass hier nicht einfach nur ein statistischer Zufallseffekt dahintersteckt. Hier ist ein solcher weiterer Beleg:

Es gibt ja die sogenannte InEK-Datenbank, in welcher die Abrechnungen der in Deutschland in den Krankenhäusern behandelten Fälle enthalten sind (datenbrowser.inek.org). Diese Datenbank hat nun Tom Lausen hinsichtlich des Auftretens von abgerechneten Fällen mit diagnostizierten Impfschäden analysiert. Tom Lausen kennen Sie vermutlich, er wurde wegen seinen Analysen zur Belegung der Krankenhausbetten sehr bekannt. Im diesem Video stellt er ab ca. 10:00 seine Ergebnisse vor:

Grob zusammengefasst: Er hat die Fälle mit den laut Abrechnungsdiagnose (ICD-Kodierung) offiziell als Impfschäden abgerechneten Fällen gezählt, und die Fallzahlen zwischen den Jahren 2019, 2020 und 2021 verglichen. Eine Anmerkung: Auch hier gibt es nach wie vor eine Dunkelziffer, das sind nur die Fälle, die offiziell mit der Diagnose „Impfschaden“ abgerechnet wurden.

Im Vergleich zu den Vorjahren ist die Anzahl der abgerechneten Fälle mit der Diagnose „Impfschaden“ von knapp 1000 auf knapp 19.000 gestiegen, 2.153 davon landeten auf Intensivstation.

Von einem Twitterer wurde das graphisch noch genauer ausgewertet hinsichtlich des zeitlichen Zusammenhangs mit den Impfungen:   hier die Graphik:

Es gibt also einen sehr hohen zeitlichen Zusammenhang zwischen den stationär mit der Diagnose „Impfschaden“ aufgenommenen Fällen und der Anzahl der COVID-Impfungen. Auch diesbezüglich kann man sich den Fehlschluss in Ihrem Twitter-Beitrag noch einmal klar machen: Einfach aus der Tatsache, dass es sich bei der Anzahl der Impfungen und der Anzahl der mit der Diagnose "Impfschaden" stationär im Krankenhaus aufgenommenen Fälle um nicht stationäre Zeitreihen handelt, zu schließen, der Zusammenhang wäre „spurious“ und somit der zeitliche Zusammenhang der Impfungen mit den stationär aufgenommenen Impfschäden Zufall, ist wissenschaftlich gesehen ganz einach unzulässig.

Schließlich möchte ich Sie noch auf einen Punkt hinweisen, den Sie offenbar übersehen haben. Sie scheinen zu meinen, ich würde aus der Höhe der Korrelationen starke Schlüsse über die Stärke der Zusammenhänge ziehen. Das ist allerdings nicht richtig. Wenn Sie mein Paper genauer lesen, heißt es dort (S. 8):

„Hinsichtlich der Stärke des statistischen Zusammenhangs werden aktuell komplexere statistische Verfahren gerechnet, welche die Zeitverzögerung der Effekte und weitere mögliche Einflussfaktoren berücksichtigen. Allerdings liefern bereits einfache Korrelationsanalysen Hinweise auf extrem starke Zusammenhänge, welche aber noch mit Vorsicht interpretiert werden müssen.“

Abschließend möchte ich Sie gerne noch etwas fragen: Sie schreiben in Ihrem Twitterbeitrag in meinen Augen sehr voreingenommen und diffamierend über mich. Mich würde sehr interessieren, wie Sie zu solchen voreingenommenen negativen Bewertungen kommen. In meinen Augen haben solche Dinge in einem echten wissenschaftlichen Diskurs nichts zu suchen.

Ich würde mich sehr freuen, wenn Sie mir noch einmal antworten könnten und dabei diesmal wirklich auf meine Argumente eingehen könnten.

Herzliche Grüße

Christof Kuhbandner

>>> Dominik Liebl <dliebl@uni-bonn.de> 26.01.2022, 19:28 >>>

Sehr geehrter Herr Kuhbandner,

meine Kritik bezieht sich ausschließlich auf Ihre Korrelationskoeffizienten. Diese sind in ihrer Höhe falsch und nicht haltbar. Ihre Rechtfertigungsversuche zeigen, dass ich Sie nicht

überzeugen konnte. Das ist nun Ihr Problem, nicht meines. Suchen Sie sich ein Einführungsbuch zur Zeitreihenanalyse. Oder suchen Sie sich einen Statistiker oder Ökonometriker von Rang, der Ihnen diesen Teil Ihrer Analyse bestätigt.

Sie kritisieren mich (ebenso wie Hr. Homburg), dass ich mich nicht inhaltlich äußere. Meine statistische Kritik ist jedoch zentral für Ihre inhaltlichen Hypothesen, da Sie Ihre Hypothesen zu einem großen Teil auf eben jene falsch hohen Korrelationen stützen. Sollten diese falsch hohen Korrelationen für Sie nur von sekundärer Bedeutung sein, dann streichen Sie diese doch einfach.

Mit freundlichen Grüßen

Dominik Liebl

>>> Christof Kuhbandner 26.01.2022, 23:15 >>>

Sehr geehrter Herr Liebl,

es ist wirklich interessant zu hören, dass sich Ihre Kritik ausschließlich auf die berichteten Korrelationskoeffizienten bezieht. Wie ich Ihnen ja bereits geschrieben habe, werden in meinem Analysepapier den berichteten Korrelationskoeffizienten explizit keine größere Bedeutung zugemessen, ich zitiere für Sie noch einmal aus meinem Papier (S. 8):

„Hinsichtlich der Stärke des statistischen Zusammenhangs werden aktuell komplexere statistische Verfahren gerechnet, welche die Zeitverzögerung der Effekte und weitere mögliche Einflussfaktoren berücksichtigen. Allerdings liefern bereits einfache Korrelationsanalysen Hinweise auf extrem starke Zusammenhänge, welche aber noch mit Vorsicht interpretiert werden müssen.“

Und ich gehe davon aus, dass Ihnen als Experte in Wirklichkeit absolut bewusst ist, dass es sich bei Ihrer Aussage, die Korrelationskoeffizienten wären in ihrer Höhe definitiv falsch, in Wirklichkeit um keine wissenschaftlich valide Schlussfolgerung handelt, sondern um eine bloße Spekulation. Sobald eine nicht stationäre Zeitreihe eine zweite Zeitreihe kausal erzeugt, ist diese notwendigerweise ebenso nicht stationär, und in diesem Fall wäre es inhaltlich einfach falsch zu schlussfolgern, hier würde die Korrelation aufgrund des Vorhandenseins von nicht stationären Zeitreihen überschätzt. Und da man den beobachteten Zusammenhängen zwischen der Übersterblichkeit und den Impfungen zumindest mittels eines einfachen statistischen Blicks nicht ansehen kann, ob zufällige Zeitreiheneffekte oder tatsächliche kausale Effekte dahinterstecken, kann man mit ihrem rein statistischen Argument hier im Grund einfach gar nichts schließen, außer der nun wirklich trivialen Aussage, dass Korrelation nicht Kausalität bedeuten muss. Das ist nun aber wirklich triviales Wissen, und genau aus diesem Grund wurden ja beispielsweise die zusätzlichen Bundeslandanalysen in meinem Papier gemacht, in Anlehnung an die aktuell gängigen Methoden im Bereich der medizinischen Forschung zur Ableitung kausaler Zusammenhänge aus beobachteten Korrelationen (siehe z.B. folgender Artikel im Deutschen Ärzteblatt). 

Wenn sich ihre „Kritik“ hier wirklich nur auf das Problem der Interpretation von Korrelationskoeffizienten bezieht, auf welches ich auch explizit immer wieder hinweise (z.B. in der Kurzzusammenfassung: "Es handelt sich um korrelative Befunde, die hinsichtlich kausaler Schlussfolgerungen vorsichtig zu interpretieren sind."), frage ich mich wirklich sehr, wie Sie eigentlich solche Aussagen wie "Meine Timeline hat mir heute ein gruselig schlechtes Paper angespült." rechtfertigen wollen.

Ich finde solche Aussagen ja schon an sich zutiefst fragwürdig und in wissenschaftlichen Diskursen absolut fehl am Platz. Aber das ist umso mehr der Fall, wenn sich herausstellt, dass solche Aussagen bei einer genaueren Betrachtungsweise offenbar - wir können hier gerne noch weiter diskutieren - mit keinerlei stichhaltigen Argumenten begründet sind.

Leider haben Sie ja meine Frage danach, warum Sie in Ihrem Twitter-Beitrag so voreingenommen und diffamierend schreiben, nicht beantwortet. Was auch immer Ihre Beweggründe sind, ich würde es für absolut angemessen halten, dass Sie diese Aussagen selbst richtigstellen und sich für die diffamierenden Äußerungen entschuldigen. Das ist meiner Meinung nach das Mindeste, was moralisch-ethisch geboten wäre - nicht nur gegenüber mir, sondern insbesondere auch gegenüber den Menschen, die ihren Aussagen folgend von einer Sicherheit der Impfstoffe ausgehen, die womöglich in Wirklichkeit nicht gegeben ist.

Mit freundlichen Grüßen,

Christof Kuhbandner

>>> Dominik Liebl <dliebl@uni-bonn.de> 26.01.2022, 23:56 >>>

Sehr geehrter Herr Kuhbandner,  

Sie betonen:

„Allerdings liefern bereits einfache Korrelationsanalysen Hinweise auf extrem starke Zusammenhänge, welche aber noch mit Vorsicht interpretiert werden müssen.“

Ich wiederhole mich:

Sie haben keine „extrem starken“ Zusammenhänge, sondern Scheinkorrelationen, welche noch nicht einmal mit Vorsicht interpretiert werden dürfen. Das ist keine Spekulation, das ist mathematischer Fakt. Sie tappen in einen klassischen Statistikfehler und wollen es nicht sehen. Mit solch einem fehlerhaften vorgehen besteht man keine Bachelorarbeit zum Thema Zeitreihenanalyse. 

Ich wiederhole mich. Sie wiederholen sich. Ich argumentierte als Experte in meinem Fach. Es ist Ihr Recht, mir nicht zu glauben. Ich denke, wir kommen an diesem Punkt nicht weiter. 

Mit freundlichen Grüßen

Dominik Liebl

=================

Was bedeutet Liebls Vorschlag?

Das war also die Unterhaltung der beiden Statistik Experten. Liebl wiederholt seinen Vorwurf der Scheinkorrelation. Und er macht einen einzigen konkreten Vorschlag. Den hier:

"Transformieren Sie die nicht-stationären Zeitreihen in stationären Zeitreihen mittels Differenzenbildung. Die ursprünglichen Zeitreihen werden so verwandelt in Zeitreihen von Änderungen. Korrelieren Sie dann die stationären Zeitreihen miteinander. Erst dann berechnen sie eine Korrelation und keine Scheinkorrelation." 

Ich habe Christof Kuhbandner gebeten, zu erklären, was Liebl hier vorschlägt und ihn gefragt, ob das tatsächlich zutrifft.

Hier seine Erklärung:

Zunächst zur allgemeinen Funktionsweise der Methode der Differenzbildung:

 

Die Grundidee dabei ist, dass man damit bestehende längerfristige zeitliche Trends, welche nicht mit der lokalen Variation von Tag zu Tag zusammenhängen, beseitigen kann. Ein einfaches Beispiel ist der Verlauf der Temperaturentwicklung: Diese setzt sich aus zwei Effekten zusammen: (1) der lokalen Variation von Tag zu Tag und (2) dem längerfristigen saisonalen Trend, der dazu führt, dass die Temperaturen beispielsweise vom Winter zum Frühling unabhängig von der lokalen Variation von Tag zu Tag langsam ansteigen.

 

Bei der Differenzbildung wird nun von Tag zu Tag berechnet, wie sich die Temperatur von einem auf den nächsten Tag verändert. Damit bleibt in der Zeitreihe der Temperaturentwicklung nur die lokale Variation von Tag zu Tag übrig, weil es dafür beispielsweise egal ist, ob die Temperatur von einem Tag auf den nächsten von 3 auf 4 Grad oder von 12 auf 13 Grad gestiegen ist.

 

Zur Logik der Anwendung bei der Analyse von zeitlichen Zusammenhängen zwischen Zeitreihen:

 

Bei der Analyse des Zusammenhangs von Zeitreihen mit jeweils bestehenden längerfristigen zeitlichen Trends gibt es nun das mögliche Problem, dass eine beobachtete Korrelation in Wirklichkeit auf die längerfristigen zeitlichen Trends zurückgeht, welche durch irgendwelche im Hintergrund existierenden Effekte generiert werden, die einen nicht interessieren, und die Variation der beiden Zeitreihen von Tag zu Tag in Wirklichkeit keine Zusammenhänge aufweisen. Dann kann man mittels der Differenzbildung die längerfristigen Trends heraus rechnen und untersuchen, ob es dann noch einen Zusammenhang auf der Ebene der lokalen Variation von Tag zu Tag gibt.

 

Zur Sinnhaftigkeit, diese Logik der Differenzbildung auf den Zusammenhang zwischen den Impfungen und der Übersterblichkeit anzuwenden:

 

Eine erste Frage ist schon einmal, ob es überhaupt Sinn macht, diese Logik der Differenzbildung bei der Analyse des Zusammenhangs zwischen den Impfungen und der Übersterblichkeit anzuwenden. Eigentlich macht die Anwendung der Methode der Differenzbildung nur Sinn, wenn es längerfristige zeitliche Trends gibt, die jeweils durch Effekte erzeugt werden, welche für die untersuchte Fragestellung uninteressant sind. Mir hat beispielsweise eine Wissenschaftlerin geschrieben, die in Ihrer Arbeit im Bereich der Geodätie sehr viel Erfahrung mit Zeitreihen-Analysen hat, und zu Liebls Argumentation meinte: 

"Ich bin ehrlich gesagt entsetzt über die Argumentation von Herrn Liebl und frage mich, ob er das, was er schreibt wirklich nicht besser weiß, oder ob er Sie einfach nur diffamieren möchte. Ersteres wäre bedenklich, letzteres absolut unkollegial". 

Hinsichtlich der Anwendung der Differenzbildung schreibt Sie:

"Eine Vorab-Filterung von Zeitreihen durch Differenzen-, Hochpass-, Tiefpass- oder andere Filter ist immer dann angezeigt, wenn ein bekannter deterministischer Effekt aus den Zeitreihen herausgerechnet werden soll, um weitere Effekte, die insbesondere durch den ansonsten vorhandenen Trend „verschluckt“ werden würden, zu detektieren.  Beispiel: Modellierung der Bodentemperatur in Abhängigkeit von Sonnenstand, Bewölkungsgrad, Niederschlag und Wind. Da die Abhängigkeit vom Sonnenstand ziemlich klar ist, würde ich hier die Daten vorab tatsächlich filtern, um anschließend die Korrelation mit Bewölkung, Niederschlag und Wind zu bestimmen. Niemand käme aber, glaube ich, auf die Idee zu behaupten, dass die Bodentemperatur nicht maßgeblich vom Sonnenstand beeinflusst wäre, nur weil beide Zeitreihen nichtstationär sind und die Korrelation eine Scheinkorrelation sei. Das wäre ungefähr so, als wenn man behauptete, dass die Öffnung eines Heizventils nur mit der Zimmertemperatur korreliert wäre, weil Ein- und Ausgangsgröße durch nichtstationäre Zeitreihen repräsentiert werden, das eine aber nicht Ursache des anderen sei."

Beim Effekt der Impfungen ist es nun so, dass es eben keinen naheliegenden deterministischen Effekt gibt, welcher für die zeitlichen Trends bei den Todesfällen bzw. bei den Impfungen verantwortlich ist. Die Saisonalität wird ja beispielsweise bei der Übersterblichkeits-Berechnung explizit aus den Daten entfernt, was im Grunde nichts anderes ist als die Beseitigung eines längerfristigen zeitlichen Trends aus den Sterbefallzahlen. Vielmehr ist das längerfristige gemeinsame Ansteigen ja genau ein Resultat eines kausalen Effektes der Impfungen. Man entfernt mit dieser Methode - insbesondere wenn man sie so simpel anwendet wie von Liebl oder den Unstatistikern vorgeschlagen - also praktisch den Effekt, den man eigentlich nachweisen möchte, weil dann praktisch nur die Effekte der Impfungen übrig bleiben, die am selben Tag auftreten.

Das kann man ganz einfach anhand eines Beispiels illustrieren. Bei den beiden Zeitreihen in der folgenden Abbildung erzeugt die Variable 1 zu 100 Prozent kausal die Variable 2, mit einer Zeitverzögerung von drei Tagen:

Rechnet man hier eine simple Korrelation, korrelieren die beiden Variablen mit r = .84, p < .001, was den wahren Zusammenhang trotz fehlender Korrektur für die Zeitverschiebung zumindest annäherungsweise realistisch abbildet.

Macht man nun eine Differenzbildung und korreliert dann die beiden Variablen miteinander – genauso wie von Herrn Liebl vorgeschlagen – korrelieren diese mit r = -.27, also negativ, und die Korrelation ist nicht signifikant.

Wie dieses einfache Beispiel zeigt, kann die von Herrn Liebl vorgeschlagene Methode in die Irre führen. Ein mit einer Zeitverzögerung auftretender kausaler Effekt wird dann womöglich nicht nur nicht erkannt, sondern es hat sogar den Anschein, als wäre der Zusammenhang in wirklich gegenteilig.

 Allerdings kann man die Methode der Differenzbildung anwenden, um zur Sicherheit unbekannte deterministische Trends zu beseitigen, die möglicherweise jeweils unabhängig voneinander die Zeitreihe der Impfungen und der Todesfälle beeinflussen und zufällige Korrelationen erzeugen. Dann muss man aber ein statistisches Modell verwenden, in welchem die möglichen Effekte der Impfungen mit unterschiedlichen zeitlichen Abständen Eingang finden. Die Analyse schätzt dann den zeitlichen Verlauf des Effektes der Impfungen mit, und man kann damit bestimmen, nach welchen Zeitabständen der Effekt der Impfungen am stärksten ist. Mit einer größeren Gruppe von Wissenschaftlern und Statistikern werden gerade solche komplexeren Analysen gerechnet, und die ersten – noch mit Vorsicht zu genießenden – Befunde bestätigen einen zeitverzögerten starken Effekt der Impfungen, auch unter Kontrolle von verschiedenen COVID-Einflussfaktoren.

=========================

Soweit die Ausführungen von Christof Kuhbandner.

Statistische Nebelbomben

Auf Kuhbandners konkrete Hinweise auf eigene Fehler in seiner Argumentation reagiert Liebl nicht. Er wiederholt stattdessen immer dasselbe Pseudo-Argument. Die Scheinkorrelation mit den vielen halblustigen Beispielen erfüllt den Zweck einer statistischen Nebelbombe. Und alle jene, die es eh schon immer gewusst haben, dass Impfungen selbstverständlich keine solchen Nebenwirkungen haben können, sind dankbar für die Schützenhilfe. 

Geklärt ist mit Liebls Ausführungen gar nichts. Ihr Zweck war es offenbar, eine entstandene Debatte über einen unerwünschten Einwand eines Wissenschaftlers abzuwürgen.

Die "Unstatistiker" vom Leibnitz Institut haben sich hierbei ebenso als opportunistische Kalmierer eingebracht, wie der Kabarettist Nuhr oder der Journalist Wolf. 

Der Versuch des Lächerlichmachens war zu erwarten. Als nächstes kommt wohl das Abstreiten. Und irgendwann haben es dann sowieso schon immer alle gewusst. 

Christof Kuhbandner macht inzwischen weiter mit seinen Analysen. Mittlerweile hat sich ein hochrangiges internationales Expertenteam gebildet. Interessante Veröffentlichungen sind zu erwarten.

Wir bleiben am Ball. 

Covid-Impfpflicht ist nur Generalprobe für weitere Zwangsimpfungen

Eine seltsame Rolle im Wettstreit der Interessen spielt die Bioethik. In Deutschland ebenso wie in Österreich stellen sich diese Kommissionen meist vollständig hinter die Covid-Maßnahmen und fordern sogar deren Verschärfung bzw. Ausweitung, Impfpflicht inklusive.

Die Juristin Christine Druml ist seit 2007 Vorsitzende der österreichischen Bioethik-Kommission. Sie hat sich bereits im Frühjahr 2020 – lange bevor es Covid-Impfungen gab – für eine Impfpflicht stark gemacht. Nun geht sie noch ein Stück weiter und sieht die Covid Impfpflicht als Generalprobe für noch ein paar weitere Impfpflichten.

Im Interview mit dem Nachrichtenmagazin Profil nennt sie Keuchhusten, Masern und Influenza als Beispiele für "überflüssige Krankheiten" und mögliche weitere Kandidaten für eine Impfpflicht. 

Zur Influenza meint sie: „Es bestehe definitiv ein gesellschaftliches Interesse daran, unnötige Grippewellen zu vermeiden.“ Druml weist darauf hin, dass die Pharmaindustrie bereits an Kombinationsimpfstoffen gegen Covid-19 und Influenza arbeitet.

Sich mit den bisherigen "Erfolgen" der Influenza-Impfung vertraut zu machen, sah Druml offenbar nicht als notwendig an. Interessant wäre beispielsweise eine im Juni 2021 publizierte Studie eines finnischen Wissenschaftlerteams zur Wirksamkeit der Influenza-Impfung in der Haupt-Risikogruppe der Menschen über 65 Jahren. Während der letzten 8 Jahre kam die Impfung dabei kein einziges Mal auf eine Wirksamkeit von zumindest 50%. 

"Influenza ist unnötig" - genügt als Argument für die Impfpflicht

In vier der acht Jahre war es zudem nicht mal gewiss, ob die Impfung vor schweren Krankheitsverläufen schützt, oder – im Gegenteil – diese sogar fördert. 

Druml weiß offensichtlich auch nicht, dass die Keuchhusten-Impfung in der internationalen Community der Impfexperten heftig unter Beschuss steht, weil sie - wenn überhaupt - nur sehr kurz wirkt. Seit vor rund 25 Jahren die derzeit verwendeten azellulären Impfstoffe auf den Markt kamen, hat sich zwar die Verträglichkeit gegenüber den davor verwendeten Ganz-Zell-Impfstoffen verbessert, die Wirksamkeit ist aber drastisch zurück gegangen. 

Je mehr Keuchhusten-Impfungen - umso mehr Keuchhusten-Fälle

In Österreich kletterten die Keuchhusten-Fälle von einem Minimum zur Jahrtausendwende bis 2019 massiv an und erreichten das Niveau der Zeit vor den Impfungen. Und das trotz ständiger Ausweitung der Impfdosen - mit Booster im Volksschulalter - und für Erwachsene (alle 10 Jahre, bzw. alle 5 Jahre ab dem Alter von 60 Jahren).

Weltweit ist die Lage ähnlich. Aus den USA werden regelmäßig Keuchhusten-Ausbrüche an Schulen gemeldet, die eine Impfquote von 100% aufweisen. "Auf Basis der aktuellen Wirksamkeit der Keuchhusten Impfung ist anzunehmen, dass jeder Mensch - ob geimpft oder ungeimpft - zumindest einmal im Leben eine Keuchhusten-Erkrankung durchmacht", erklärt der Münchner Kinderarzt Martin Hirte.

Viel versprechende Versuche, eine Keuchhusten-Lebendimpfung zu entwickeln, stocken seit vielen Jahren, obwohl die Resultate im Tierversuch  und ersten Studien am Menschen eine hohe Wirksamkeit bei guter Verträglichkeit ergeben haben. "Doch wir bekommen kaum Förderungen - speziell die Konzerne sind leider wenig daran interessiert, in Forschung zu investieren", erklärte mir Camille Locht, die Leiterin eines französischen Wissenschaftler-Teams der Universität Bordeaux, die seit Jahren an einer inhalierbaren Pertussis-Lebendimpfung forscht. 

"Vaccinology" gleicht zunehmend einer Sekte

Nennenswerte Recherche braucht es für "Bioethikerin" Druml offensichtlich nicht, um sich ein Bild zu machen. Je größer der Glaube an die segensreiche Wirkung der Impfungen ist, desto schneller wird der Ruf nach einer Impfpflicht laut. Denn schließlich sollen alle an den Segnungen teil haben. Auch jene, die zu dumm sind, das Impfmirakel zu erkennen. 

Die „Wissenschaft“ vom Impfen wird immer mehr zum Magnet für Gläubige und Populisten, denen es darum geht, das historisch erworbene gute Image für ihr eigenes Ansehen zu nutzen, oder ihm zu huldigen. 

Dass jede Impfung anders ist wird dabei ignoriert. 

Auf komplizierte Details, dass es sich z.B. bei der mRNA-Technik um ein vollständig neuartiges Verfahren handelt, das mit der bisher verwendeten Definition von Impfstoffen kaum noch etwas gemeinsam hat, will sich weder Druml noch sonst jemand aus der Clique einlassen. Wichtiger ist es, das Markenzeichen "Impfung" zu pflegen und alle Kritik vorsorglich nieder zu machen. 

So schart sich ein Rudel Gläubiger um die Vaccinology und fordert, dass ihre Religion – mittels Pervertierung des bisherigen Verständnisses von Wissenschaft – zur Staatsreligion erklärt wird.  Ungläubige müssen bestraft und notfalls zwangs-getauft werden. 

PS: Wenn Dir dieser Blog interessant und wichtig erscheint, dann bitte abonniere ihn. Eine einmalige oder regelmäßige Spende unterstützt meine Arbeit sehr.

Bert Ehgartner steht auch für Vorträge, Filmvorführungen, etc. zur Verfügung. 
Nähere Informationen finden Sie auf dieser Seite. 

Von Laer und Wagner: das Dream-Team der Covid-Dauerkrise

Der Mikrobiologe Michael Wagner und die Virologin Dorothee von Laer sind Dauergäste in den Medien, wo sie ohne kritische Gegenfragen ihre kruden Thesen verbreiten dürfen, die alle in eine Richtung laufen: Ein möglichst striktes Lockdown-Regime, Dauer-Testen, Booster-Impfen, Masken tragen.

Von Laer ist mittlerweile berühmt für ihr resolutes Covid-Regime, etwa ihre Vorschläge, die 1G-Regel einzuführen, Schulen zu sperren, "als eine der effizientesten Lockdown-Maßnahmen" oder ihre Forderung, Tirol abzusperren, um damit die Verbreitung von Virus-Varianten zu unterbinden. Delta brauchte rund 4 Wochen, um global zur dominierenden Viren-Variante zu werden. Wie lange hätte van Laers Vorschlag, die Tiroler einzusperren, diesen viralen Siegeszug wohl verlangsamt: um Stunden? Minuten?

Nun fordert die mittlerweile hauptsächlich auf ihrem Gestüt im Burgenland logierende Virologin in mehreren Interviews, es den Deutschen gleich zu tun und die Gültigkeit des "Genesen"-Status im Grünen Pass auf die Hälfte (3 Monate) zu reduzieren. Sie nannte dafür nebulos "eine Studie", die das nahelegen würde. Die diversen Redakteure fragten nicht näher nach. Offenbar ist es Beweis genug, wenn eine Professorin etwas sagt.

Ähnlich die Argumentation des Mikrobiologen Michael Wagner. Er wettert verlässlich gegen alle Erleichterungen von Covid-Maßnahmen, so als wäre er persönlich an der Aufrecht-Erhaltung des Pandemie-Regimes gewinnbringend beteiligt.
Nun gehen ihm die Abschaffung der Masken beim Turnen sowie die Aufhebung der Maskenpflicht für Volksschüler während des Unterrichts gegen den Strich. Er wäre dafür, "damit bis Ostern zu warten", erklärte er gegenüber ORF-Wien. Auch bei ihm gilt Bauchgefühl als oberste wissenschaftliche Expertise. Denn jetzt „werden sich sicherlich mehr Kinder anstecken als mit Masken“.

Mikrobiologe Michael Wagner wurde bekannt als Promoter der Gurgeltests

Auch hier wurden vom Reporter keinerlei wissenschaftliche Begründungen verlangt, was denn schlecht daran wäre, wenn sich Kinder mit den für sie harmlosen Omicron-Viren infizieren und fortan eine sterile Immunität genießen - ganz im Gegenteil zu den Geimpften.
Niemand kam auf die Frage, Wagner mit dem Beispiel Schweden zu konfrontieren, wo es nie Maskenpflicht für Schüler gab. Oder mit Dänemark, der Schweiz, England und anderen Ländern, die trotz deutlich weniger rigiden Covid-Maßnahmen keine schlechteren Zahlen haben als Österreich. Im Gegenteil.

Es ist auch ein Zeichen von Intelligenz, in der Wahl der Experten und Berater vorsichtig zu sein und nicht Extremisten eine ständige Hauptrolle anzubieten. Das gilt für die Politik ebenso wie die Mehrzahl der Medien.

PS: Wenn Dir dieser Blog interessant und wichtig erscheint, dann bitte abonniere ihn. Eine einmalige oder regelmäßige Spende unterstützt meine Arbeit sehr.

Bert Ehgartner steht auch für Vorträge, Filmvorführungen, etc. zur Verfügung. 
Nähere Informationen finden Sie auf dieser Seite.